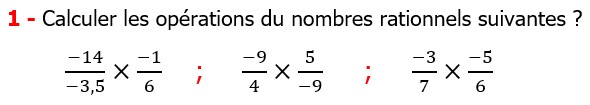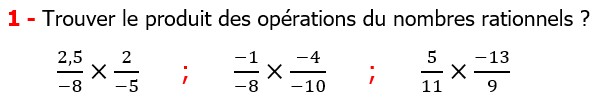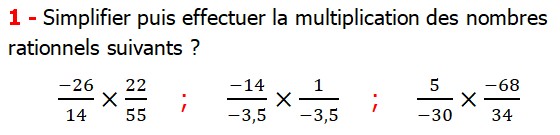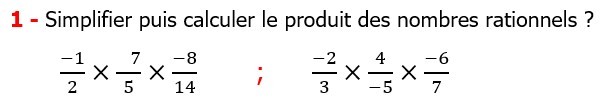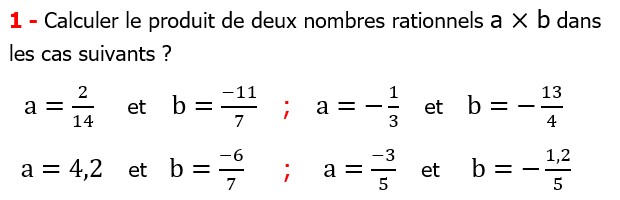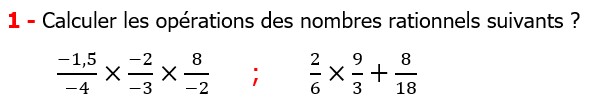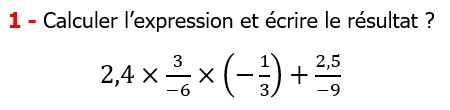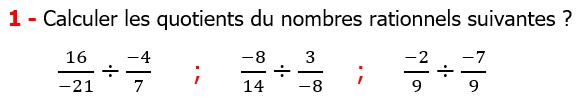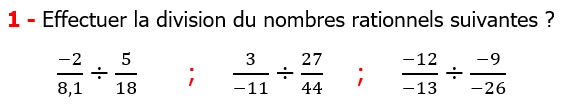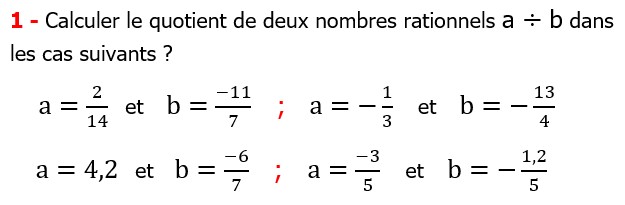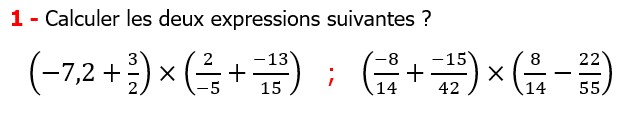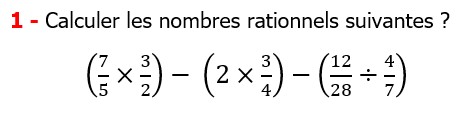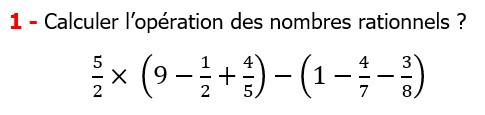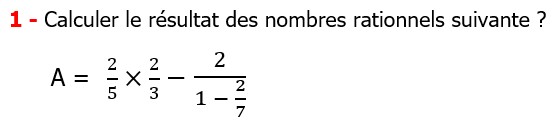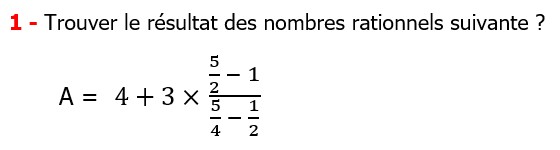Exercices corrigés les nombres rationnels multiplication et division maths 3éme
| EXERCICE DE MATHS 1 | Les nombres rationnels Multiplication et Division |
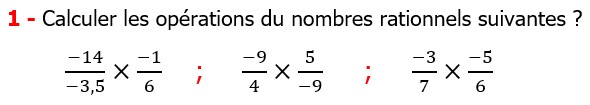
CORRECTION EXERCICE DE MATHS 1
| EXERCICE DE MATHS 2 | Les nombres rationnels Multiplication et Division |
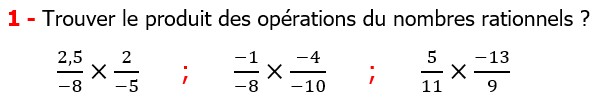
CORRECTION EXERCICE DE MATHS 2
| EXERCICE DE MATHS 3 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 3
| EXERCICE DE MATHS 4 | Les nombres rationnels Multiplication et Division |
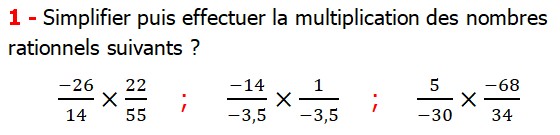
CORRECTION EXERCICE DE MATHS 4
| EXERCICE DE MATHS 5 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 5
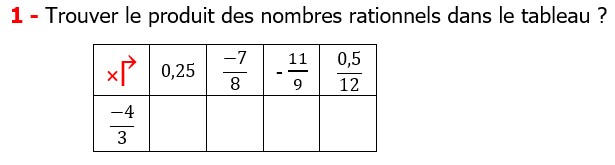
| EXERCICE DE MATHS 6 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 6
| EXERCICE DE MATHS 7 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 7
| EXERCICE DE MATHS 8 | Les nombres rationnels Multiplication et Division |
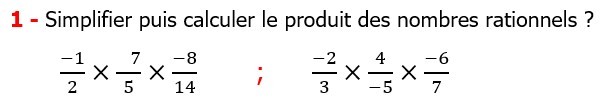
CORRECTION EXERCICE DE MATHS 8
| EXERCICE DE MATHS 9 | Les nombres rationnels Multiplication et Division |
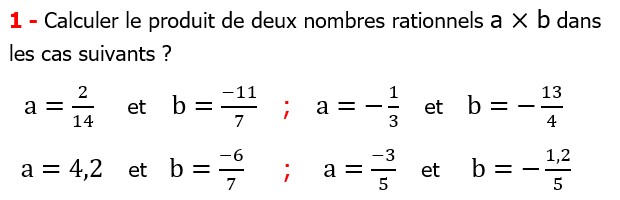
CORRECTION EXERCICE DE MATHS 9
| EXERCICE DE MATHS 10 | Les nombres rationnels Multiplication et Division |
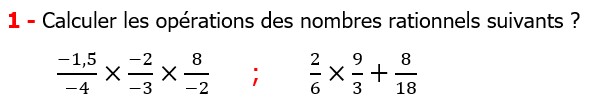
CORRECTION EXERCICE DE MATHS 10
| EXERCICE DE MATHS 11 | Les nombres rationnels Multiplication et Division |
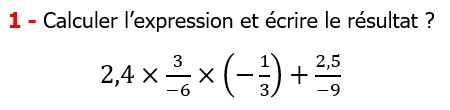
CORRECTION EXERCICE DE MATHS 11
| EXERCICE DE MATHS 12 | Les nombres rationnels Multiplication et Division |
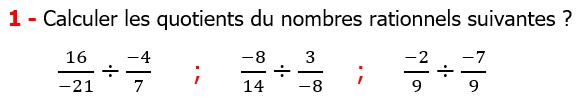
CORRECTION EXERCICE DE MATHS 12
| EXERCICE DE MATHS 13 | Les nombres rationnels Multiplication et Division |
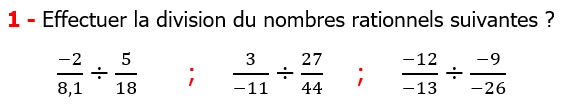
CORRECTION EXERCICE DE MATHS 13
| EXERCICE DE MATHS 14 | Les nombres rationnels Multiplication et Division |
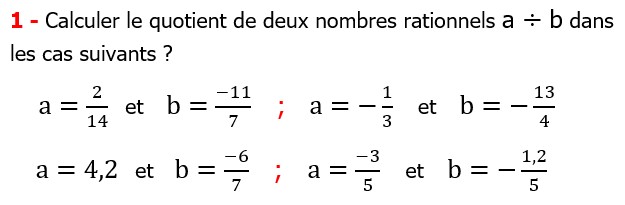
CORRECTION EXERCICE DE MATHS 14
| EXERCICE DE MATHS 15 | Les nombres rationnels Multiplication et Division |
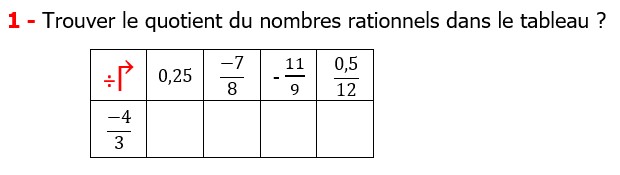
CORRECTION EXERCICE DE MATHS 15
| EXERCICE DE MATHS 16 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 16
| EXERCICE DE MATHS 17 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 17
| EXERCICE DE MATHS 18 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 18
| EXERCICE DE MATHS 19 | Les nombres rationnels Multiplication et Division |
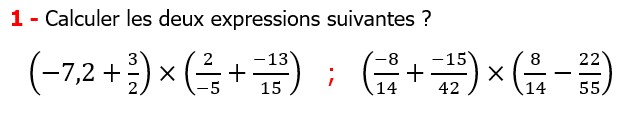
CORRECTION EXERCICE DE MATHS 19
| EXERCICE DE MATHS 20 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 20
| EXERCICE DE MATHS 21 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 21
| EXERCICE DE MATHS 22 | Les nombres rationnels Multiplication et Division |
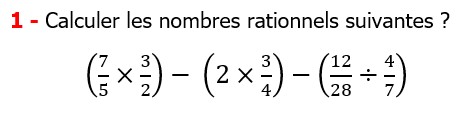
CORRECTION EXERCICE DE MATHS 22
| EXERCICE DE MATHS 23 | Les nombres rationnels Multiplication et Division |
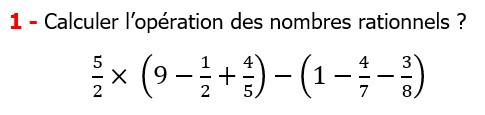
CORRECTION EXERCICE DE MATHS 23
| EXERCICE DE MATHS 24 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 24
| EXERCICE DE MATHS 25 | Les nombres rationnels Multiplication et Division |
CORRECTION EXERCICE DE MATHS 25
| EXERCICE DE MATHS 26 | Les nombres rationnels Multiplication et Division |
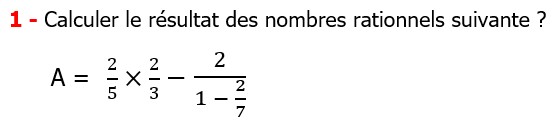
CORRECTION EXERCICE DE MATHS 26
| EXERCICE DE MATHS 27 | Les nombres rationnels Multiplication et Division |
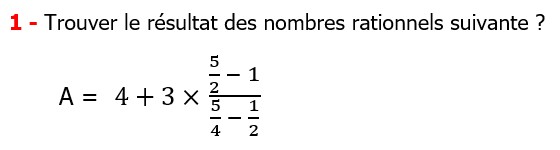
CORRECTION EXERCICE DE MATHS 27
| FICHES DE MATHÉMATIQUES POUR LE NIVEAU TROISIÈME |